Batch 3 - Class 228 - Magic Squares
(Zoom)
Pre-Class Exercise
- A 15-inch-long stick has four marks on it, dividing it into five segments of length 1,2,3,4 and 5 inches (although not necessarily in that order) to make a "ruler. Example below - using this ruler, you could measure 8 inches (between B and D) but you couldn't measure 12 inches. Prove that it is impossible to place the four marks in a manner that you can measure all integers 1 inch through 15 inches.
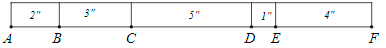
- Answer: There are only 15 measurements that can be made with 4 marks, and hence each number should be measurable exactly once. If 1 is next to 2,3 or 4, then there would be multiple ways of measuring 3, 4 and 5 respectively. So 1 has to be next to 5. Similarly, if 2 were next to 3 or 4, we would not have multiple ways of measuring 5 or 6, so 2 must also be next to 5. But this means that 1 or 2 can't both be at the extreme ends, which would make it impossible to measure 13 and 14. Hence proved.
Attendance Kabir, Aarkin, Vansh, Advay, Kushagra, Ayush, Rhea, Rohan, Anshi, Vivaan, Rehaan, Angad, Arjun N, Shikher
Class puzzles (From Class 10, plus some extensions)
Magic square is a n x n grid filled with numbers from 1 to n^2, non-repeating, such that every row, every column, and each of the two diagnols have the same sum.
Draw a 3x3 Magic square
Instructor Notes: Check that each kid has understood the meaning of magic square. Let kids try and draw a 3x3 magic square by hit and trial. After that, go methodically to see all combinations of sums of 1-9 which total to 15, and how to lay those out on a magic square.
Story of Divine Tortoise: There was recurrent flooding in river Lo. Emporer Yu-Huang was standing by a river, and saw a divine turtle at his feet. He believesd that it was a symbol of good luck. Slowly, the details of the shell appeared before the emperor. Emperor Yu looked at the turtle's back and noticed a pattern of dots engraved on it. Emperor Yu thought about whether the turtle was giving a signal? He added up the numbers many different ways, and they all added up to 15. He then offered 15 sacrifices, and that took the floods away.
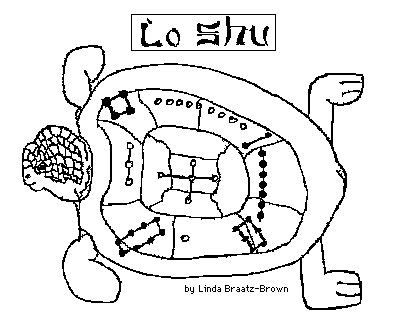
- Join the numbers on magic square in order, and see the pattern.
- If you see the line connceting 8-5-2, what is the symmetry.
- Calculate the difference of 5 with every other number and see what happens.
- Method to create magic squares of odd order
- Start from center square on top row and keep going diagonally upward-right. If you can't go there, go down. Wrap around the squares like a torus.
- Why does this work (intuitively)
- Can you create the Lusha using this method? 7x7 magic square?
Draw a 2x2 Magic square
Instructor Notes: Let kids arrive at the conclusion that a 4x4 magic square doesn't exist
Illustrate a 4x4 Magic squares (note that 880 of these exist) - In 1514, Albrecht Dürer created an engraving named Melancholia that included a magic square. In the bottom row of his 4 X 4 magic square you can see that he placed the numbers "15" and "14" side by side to reveal the date of his engraving.



- Join the numbers on magic square in order, and see the pattern.
- What kind of symmetry do you see?
- Can you find a formula for sum of a n x n magic square side?
Benjamin Franklin's 8x8 magic square with lines

- Let kids total up the rows and columns to verify this magic square.
- Sum up the numbers half-way down the column and see what happens?
- Add the numbers on four corners - see what happens?
- Consider each of the 4x4 units - what is true of them?
- Homework: Can you find more numerical relationships?
- See the symmetry in the magic square.
- Where are numbers 1-10, where are 54-64?
- Where are 1,2,63,64 - what is the sum?
- Where are 31,32,33,34 - what is the sum?
- What is the overall symmetry in the pattern?
- Constructing 4p order magic squares - magic squares of side 4, 8, 12 and so on.
- One can do that by writing the numbers in order row by row, top to bottom. Now overlay a pattern of 1's and 0's, 1's corresponding to numbers taken as is, and 0's corresponding to ones taken in opposite order.
.png)
- The patterns are a) there are equal number of '1's and '0's in each row and column; b) each row and each column are "palindromic"; c) the left- and right-halves are mirror images; and d) the top- and bottom-halves are mirror images (c and d imply b). The pattern table can be denoted using hexadecimals as (9, 6, 6, 9) for simplicity (1-nibble per row, 4 rows). The simplest method of generating the required pattern for higher ordered doubly even squares is to copy the generic pattern for the fourth-order square in each four-by-four sub-squares.
.png)
- Other choices for 8x8 include (3C, 3C, C3, C3, C3, C3, 3C, 3C); (A5, 5A, A5, 5A, 5A, A5, 5A, A5) - can you draw the pattern?
- Order-12 has pattern (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) - can you draw the pattern?
Homework:
- There are nine cards on a table labeled by numbers 1 trough 9. Alice and Bob take turns choosing one card. The player that has collected a set of cards with the property that the sum of numbers on three cards out of total set is 15 wins. There’s a tie if none of the players has a set of cards with this property at the end of the game. Does any of the players have a winning strategy? A non-losing strategy?
- (Answer: Same as magic square and tic tac toe combined - so first player wins)
References: